[논문리뷰] SpikingResformer 및 코드 실행
- -
https://github.com/xyshi2000/SpikingResformer
GitHub - xyshi2000/SpikingResformer: Codes of the paper: SpikingResformer: Bridging ResNet and Vision Transformer in Spiking Neu
Codes of the paper: SpikingResformer: Bridging ResNet and Vision Transformer in Spiking Neural Networks (CVPR2024) - xyshi2000/SpikingResformer
github.com
https://github.com/khw11044/SpikingResformer
Abstract
ANN에서 Vision Transformers은 성공적
Spiking Neural Networks(SNNs)에 역시 self-attention mechanism과 transformer-based architecture를 통합하려는 시도가 이루어졌다.
기존 방법에 이미 SNN과 호환되는 spiking self-attention mechanisms을 제안하긴 하였음
문제점
- 합리적인 스케일링(?) 방법이 부족
- 제안된 전체 아키텍처로는 local features를 효과적으로 추출하는데 있어 병목현상을 겪음
문제 해결 방안, 제안
- 합리적인 스케일링 방법을 갖춘 새로운 spiking self-attention mechanism인 Dual Spike Self-Attention (DSSA)을 제안
- ResNet-based multi-stage architecture와 DSSA를 결합한 새로운 spiking Vision Transformer architecture인 SpikingResformer를 제안
결과
- 다른 spiking Vision Transformer 와 비교하여 더 적은 파라미터와 에너지 소비로 더 높은 정확도를 달성
- 성능과 에너지 효율성을 모두 개선
- 파라미터 수 줄임
- SpikingResformer-L은 4 time-steps으로 ImageNet에서 79.40%의 top-1 accuracy를 달성
- SNN 분야 최성능 달성

Introduction
Spiking Neural Networks (SNNs)은 인공신경망(ANNs)의 3세대 모델로 간주된다.
특징
- 낮은 전력 소비,
- 생물학적 타당성,
- neuromorphic 하드웨어와 호환되는 event-driven 특성
과 같은 장점 덕분에 큰 주목을 받고 있다
SNNs에 트랜스포머 구조를 통합하는 주요 문제점은 SNNs에 적합한 self-attention mechanism을 설계하는 것이다.
ANNs에서 사용되는 vanilla self-attention mechanism은
- 부동소수점 행렬 곱셈(float-point matrix multiplication)과 소프트맥스 연산(softmax operations) 사용
이러한 연산은 부동 소수점 곱셈, 나눗셈, 지수 연산을 포함하고 있으며 SNNs의 Spike 기반 특성에 맞지 않는다.
또한, ANN 트랜스포머에서 일반적으로 사용되는 layer normalization (LN)와 GELU 활성화 함수는 SNNs에 직접 적용될 수 없다.
따라서 트랜스포머 아키텍처를 SNNs에 도입하려면 이러한 연산을 우회하고, SNNs의 고유한 요구 사항을 충족시킬 필요가 있다.
기존 방법론들의 문제점
- 부동 소수점 연산을 부분적으로 유지하거나, SNN과 ANN 트랜스포머를 병렬로 실행하는 접근법은 성능을 향상시키지만, 기본적인 셀프 어텐션과 SNNs 간의 비호환성을 완전히 해결하지는 못하였다.
- synaptic operations과 fully spike-driven 기반 spiking self-attention mechanisms과 spiking Vision Transformer 아키텍처를 제안하는 연구는 셀프 어텐션 메커니즘과 SNNs 간의 비호환성을 완벽히 해결하고, 기존의 스파이킹 컨볼루션 신경망보다 훨씬 뛰어난 성능을 보여주었다.
그러나 이러한 방법들의 spiking transformer 아키텍처는 로컬 특징을 추출하는 데 병목 현상을 보인다.
Transformer encoder 이전에 얕은 컨볼루션 네트워크를 사용하여 로컬 특징을 추출하고, 특징 맵의 크기를 줄이지만, 이 얕은 네트워크의 효율성은 Transformer encoder에 비해 제한적이다.
이 얕은 네트워크를 Transformer encoder로 대체하는 것은 불가능하다.
그 이유는 이들의 spiking self-attention mechanisms이 합리적인 스케일링 방법을 갖추고 있지 않아, 작은 특징 맵에만 적합하기 때문이다.
이러한 메커니즘에 적합한 스케일링 요소를 설계하는 것이 어려운 이유는 self-attention을 생성하는 뉴런으로의 입력 전류가 단순한 평균과 분산 형태를 가지지 않기 때문이다. 대규모 특징 맵을 효과적으로 처리할 수 있는 합리적인 스케일링 방법을 갖춘 새로운 spiking self-attention mechanism을 설계하는 것이 시급하다.
해결 방법 제안
이러한 문제를 해결하기 위해 Dual Spike Self-Attention (DSSA)이라는 새로운 spiking self-attention mechanism을 제안한다.
DSSA는 Dual Spike Transformation을 통해 스파이킹 셀프 어텐션을 생성하며, 완전히 스파이크로 구동되고 SNNs와 호환되며, 직접적인 스파이크 곱셈의 필요성을 제거한다.
또한, DSSA에서 사용되는 스케일링 방법을 자세히 설명하여, 임의 크기의 특징 맵에도 적응할 수 있게 한다.
DSSA를 기반으로 우리는 SpikingResformer라는 새로운 spiking Vision Transformers 아키텍처를 제안한다.
이 아키텍처는 ResNet 기반의 multi-stage design을 우리의 spiking self-attention mechanism과 결합한 것이다.
요약 및 주요 기여
- 우리는 새로운 스파이킹 셀프 어텐션 메커니즘인 Dual Spike Self-Attention (DSSA)을 제안한다. DSSA는 Dual Spike Transformation을 통해 스파이킹 셀프 어텐션을 생성하며, 완전히 스파이크 기반으로 동작하고 SNNs와 호환된다.
- DSSA에서 사용된 스케일링 요소들을 상세히 설명하여, DSSA가 임의의 크기의 특징 맵을 처리할 수 있게 하였다.
- 우리는 ResNet 기반의 다중 스테이지 아키텍처와 DSSA를 결합한 SpikingResformer 아키텍처를 제안한다.
- 실험 결과, 제안한 SpikingResformer는 다른 스파이킹 비전 트랜스포머보다 적은 파라미터와 더 낮은 에너지 소비로 성능이 크게 향상됨을 보여줍니다. 특히, 우리의 SpikingResformer-L은 ImageNet에서 최대 79.40%의 Top-1 정확도를 달성하였다.
2. Related Work
Spiking convolutional neural networks (SCNNs)은 surrogate gradient learning의 놀라운 성공 덕분에 광범위하게 개발되었으며, 객체 인식, 탐지, 세분화와 같은 도전적인 비전 작업을 처리하는 데 널리 사용되고 있습니다.
Surrogate Gradient Learning in Spiking Neural Networks
SCNNs의 성능을 향상시키기 위한 노력으로 훈련 방법과 ANN-to-SNN 변환 기법을 탐구하였다.
- SpikingVGG의 성공은 SCNNs가 인식 작업에서 ANNs와 비교할 만한 성능을 달성할 수 있음을 보여주었다.
- SpikingResNet은 SCNNs의 residual structures를 탐구하고 ResNet 기반 아키텍처를 통해 더 깊은 SCNN을 달성하였다.
- SEW ResNet은 directly-trained spiking residual networks에서 identity mapping을 분석하고, 152-layer SCNN을 직접 훈련하였다.
이러한 아키텍처들은 많은 층을 가진 대규모 SNNs를 활용하여 다양한 작업에서 뛰어난 성능을 보여주었다.
Spiking Vision Transformers
Spikformer[2023년]는 pure SNN architecture를 갖춘 최초의 spiking vision transformer이다.
Spikformer는 Query, Key, 그리고 Value를 spiking neurons으로 활성화하고 softmax를 spiking neurons으로 대체하여 곱셈을 제거한 spiking self-attention mechanism을 도입하였다.
또한, Transformer에서 ‘Layer Normalization과 GELU activation’을 Batch Normalization과 spiking neurons으로 대체하였다.
Spikformer를 기반으로 한 Spikingformer는 residual connection 패러다임을 수정하여 완전히 스파이크 기반으로 동작하는 비전 트랜스포머를 달성하였다. Spike-driven Transformer는 선형 복잡도의 spike-driven self-attention mechanism을 제안하여 에너지 소비를 효과적으로 줄였습니다. 그러나 이러한 모든 시도는 patches의 sequence를 형성하기 위해 로컬 정보를 사전에 추출하는 얕은 컨볼루션 네트워크를 사용하며, 적절한 스케일링 방법이 결여되었다.
3. Preliminary
본 논문에서 사용된 Leaky Integrate-and-Fire (LIF) 뉴런의 동작은 다음 discrete-time model로 설명한다.
$$ v_i[t] = u_i[t] + \frac{1}{\tau} \left(I_i[t] - (u_i[t] - u_{\text{rest}})\right) $$
$$ s_i[t] = H(v_i[t] - u_{\text{th}}) $$
$$ u_i[t + 1] = s_i[t] u_{\text{rest}} + (1 - s_i[t]) v_i[t] $$
방정식 (1)은 charging process을 설명합니다.
여기서 $u_i[t]$와 $ v_i[t] $는 각각 충전 전후의 $i$-번째 시냅스 후 뉴런(postsynaptic neuron)의 막 전위(membrane potential)를 나타냅니다.
$\tau $는 막 시간 상수(membrane time constant)입니다.
$I_i[t] $는 입력 전류를 나타내며, 일반적으로 $ I_i[t] = \sum_j w_{i,j} s_j[t] $로 나타낼 수 있습니다.
여기서 $ s_j[t] \in {0, 1} $은 $t$ 시점의 $j$-번째 시냅스 전 뉴런의 스파이크 출력을 나타내며, $w_{i,j} $는 뉴런 $j$에서 뉴런 $i$로의 시냅스 연결의 가중치를 나타냅니다.
방정식 (2)은 발화 과정을 설명하며, 여기서 $ H(\cdot) $은 헤비사이드 함수, $s_i[t] \in {0, 1} $는 스파이킹 뉴런의 스파이크 출력, $ u_{\text{th}} $는 발화 임계값을 나타냅니다.
방정식 (3)은 리셋 과정을 설명하며, $u_{\text{rest}} $는 휴지 전위를 나타냅니다.
후속 섹션의 간결함과 명확성을 위해, 스파이킹 뉴런 모델을 다음과 같이 나타냅니다:
$$S = \text{SN}(I)$$
여기서 $ \text{SN}(\cdot) $은 뉴런 내부의 동적 과정을 생략한 스파이킹 뉴런 계층을 나타내며, $ I \in \mathbb{R}^{T \times n} $은 입력 전류(여기서 $T$는 시간 스텝, $n$은 뉴런의 수), $( S \in {0, 1}^{T \times n} )$은 해당 스파이크 출력을 나타냅니다.
간단하게 다시 설명하면 본 논문에서 사용한 Leaky Integrate-and-Fire (LIF) 뉴런의 동작은 discrete-time model로 설명가능하며, I 입력 전류가 입력되면 0과 1 둘중 하나의 값을 갖는 집합 S가 출력된다. 를 배경지식으로 알고가자. 사실 LIF에 대해 그리고 SNN에 대해 더 자세히 공부하면 알 수 있겠다.
4. Dual Spike Self-Attention
이 섹션에서는 먼저 ANNs에서 일반적으로 사용되는 기본적인 셀프 어텐션(VSA) 메커니즘을 다시 살펴보고, VSA가 왜 SNNs에 적합하지 않은지 분석한다.
그런 다음 호환성을 위해 특별히 설계된 Dual Spike Self-Attention (DSSA)을 제안한다.
마지막으로 DSSA에서 스케일링 요소의 중요성과 DSSA의 스파이크 구동 특성을 논의한다.
4.1. Vanilla Self-Attention
트랜스포머에서 기본 셀프 어텐션은 다음과 같이 수식화될 수 있습니다:
$$ Q = XW_Q, \quad K = XW_K, \quad V = XW_V $$
$$\text{Attention}(Q, K, V) = \text{Softmax}\left(\frac{QK^T}{\sqrt{d}}\right)V$$
여기서 $Q$, $K$, $V$는 각각 쿼리(Query), 키(Key), 밸류(Value)를 나타내며, $n$은 패치(patch)의 수, $d$는 임베딩 차원입니다.
$X$는 입력을 나타내며, $W_Q$, $W_K$, $W_V$는 각각 $Q$, $K$, $V$에 해당하는 선형 변환의 가중치 행렬입니다.
ANNs에서 사용되는 기본 셀프 어텐션은 SNNs에 적합하지 않은 두 가지 이유가 있습니다:
- 1. $Q$와 $K$ 사이의 부동 소수점 행렬 곱셈 및 어텐션 맵과 $V$ 사이의 곱셈을 포함합니다.
- 2. 소프트맥스 함수는 지수 계산과 나눗셈을 포함합니다.
이러한 연산들은 부동 소수점 곱셈, 나눗셈, 지수 계산에 의존하는데, 이는 스파이크 기반의 SNNs 특성과 호환되지 않습니다.
4.2 Dual Spike Self-Attention
SNNs에 셀프 어텐션 메커니즘을 도입하고 멀티 스케일 특징 맵을 효율적으로 처리하기 위해, 우리는 Dual Spike Self-Attention (DSSA)이라는 새로운 스파이킹 셀프 어텐션 메커니즘을 제안한다.
DSSA는 Dual Spike Transformation (DST)을 사용하여 스파이킹 셀프 어텐션을 생성하며, 부동 소수점 곱셈과 소프트맥스 함수의 필요성을 제거한다.
먼저 DST를 다음과 같이 정의합니다:
$$
\text{DST}(X, Y; f(\cdot)) = Xf(Y) = XYW
$$
$$
\text{DST}^T(X, Y; f(\cdot)) = Xf(Y)^T = XW^T Y^T
$$
식 (7)에서, $X \in \{0, 1\}^{T \times p \times m}$ 그리고 $Y \in \{0, 1\}^{T \times m \times q}$는 각각 Dual Spike 입력을 나타냅니다.
여기서 $T$는 시간 스텝, $p$, $m$, $q$는 임의의 차원을 나타냅니다.
$f(\cdot)$는 $Y$에 대한 일반화된 선형 변환을 의미하며, $W \in \mathbb{R}^{q \times q}$는 가중치 행렬입니다.
이는 $Y$에 대한 선형 변환으로, 합성곱(컨볼루션)이나 배치 정규화(Batch Normalization)와 같은 연산을 포함할 수 있습니다. 자세한 설명은 부록에 나와 있습니다.
마찬가지로, 식 (8)에서 $Y \in \{0, 1\}^{T \times q \times m}$, $W \in \mathbb{R}^{m \times m}$로 정의됩니다.
$X$와 $Y$는 모두 스파이크 행렬이므로 모든 행렬 곱셈은 가중치의 합산과 동일합니다.
따라서 DST는 부동 소수점 곱셈을 피하고, SNNs와 호환됩니다.
자 이 부분 잘 이해가 안될 수도 있으니 좀 풀어서 작성해 보았다.
Dual Spike Self-Attention(DSSA)의 DST(Dual Spike Transformation) 부분은 부동 소수점 곱셈을 피하기 위해 특별히 설계되었습니다. 이 과정을 이해하기 위해 먼저 어떻게 부동 소수점 곱셈을 피하는지 설명드리겠습니다.
1. 스파이크 기반 계산:
DSSA에서는 입력으로 스파이크 행렬을 사용합니다. 이 행렬들은 0 또는 1의 값만을 가집니다. 즉, 스파이킹 신경망에서는 부동 소수점(실수) 값 대신 이진값을 사용하여 계산을 수행합니다. 부동 소수점 곱셈을 피하는 핵심은 바로 이 스파이크 행렬입니다.
2. 행렬 곱셈:
DST에서 행렬 곱셈이 포함되는데, 이는 보통 부동 소수점 곱셈을 수반합니다. 하지만, DSSA에서는 모든 요소가 0 또는 1이기 때문에 곱셈 대신 단순한 덧셈으로 계산을 대체할 수 있습니다. 예를 들어:
- 두 스파이크 값이 1일 때만 이들의 곱셈이 1이 됩니다.
- 하나라도 0이면 그 값은 0이 되어, 해당 가중치는 더해지지 않습니다.
3. 스파이크 행렬의 논리적 AND 연산:
DST에서는 스파이크 행렬이 사용되기 때문에 행렬 곱셈에서 발생하는 값들이 사실상 논리적 AND 연산으로 해석됩니다. 즉, 두 개의 스파이크 행렬 $X$와 $Y$의 요소가 모두 1일 때만 1이 되고, 그렇지 않으면 0이 됩니다. 이는 부동 소수점 곱셈 대신 가중치의 덧셈으로 대체할 수 있는 계산으로 이어집니다.
4. 소프트맥스와 같은 부동 소수점 연산 제거:
일반적인 셀프 어텐션 메커니즘에서는 소프트맥스 연산이 필요합니다. 소프트맥스는 지수 함수와 나눗셈을 포함한 복잡한 부동 소수점 연산을 요구하지만, DSSA에서는 이러한 연산을 스파이킹 뉴런의 이진 출력으로 대체하여 연산의 복잡성을 줄입니다.
결론:
- DSSA는 이진값(0 또는 1)을 사용하는 스파이킹 행렬을 도입하여 부동 소수점 연산을 피할 수 있습니다.
- 스파이크 기반 연산에서는 부동 소수점 곱셈이 아닌 덧셈과 논리적 AND 연산으로 처리하여 부동 소수점 계산의 복잡성을 줄이면서도 효율적으로 계산을 수행합니다.
이러한 방식 덕분에 DSSA는 SNNs에서 부동 소수점 연산을 피하면서도 복잡한 어텐션 메커니즘을 효과적으로 구현할 수 있습니다.
다시 논문으로 돌아와서. "DST의 호환성과 스파이크 구동 특성에 대한 추가 논의는 4.4절에서 더 자세히 다룬다.
DST를 기반으로 DSSA의 어텐션 맵은 다음과 같이 수식화될 수 있다:
$$ \text{AttnMap}(X) = \text{SN}(\text{DST}^T(X, X; f(\cdot)) \ast c_1) $$
$$ f(X) = \text{BN}(\text{Conv}_p(X)) $$
여기서 $X \in \{0, 1\}^{T \times HW \times d}$는 스파이크 입력이고,
$H$와 $W$는 입력의 공간적 높이와 너비를 나타내며,
$d$는 임베딩 차원입니다.
$\text{BN}(\cdot)$은 배치 정규화 계층을 의미하며,
$\text{Conv}_p(\cdot)$는 스트라이드가 $p$인 $p \times p$ 합성곱을 나타냅니다.
$c_1$은 스케일링 요소입니다.
합성곱 연산은 일반화된 선형 변환과 동일하므로, 배치 정규화는 합성곱에 흡수될 수 있습니다(바이어스는 무시).
우리는 공간 크기를 줄이고 계산 오버헤드를 줄이기 위해 $p \times p$ 합성곱을 사용합니다.
DSSA에서는 스파이킹 뉴런 계층이 이진 어텐션 맵(스파이크로 구성된)을 자동으로 생성하므로 소프트맥스 함수가 필요 없습니다.
이 스파이킹 어텐션 맵의 각 스파이크 $s_{ij}$는 패치 $i$와 패치 $j$ 간의 어텐션을 나타냅니다.
우리는 이러한 스파이킹 어텐션 맵이 소프트맥스로 활성화된 ANN의 어텐션 맵보다 더 해석 가능하다고 생각합니다.
스파이킹 어텐션 맵을 사용하여 DSSA는 다음과 같이 수식화될 수 있습니다:
$ \text{DSSA}(X) = \text{SN}(\text{DST}(\text{AttnMap}(X), X; f(\cdot)) \ast c_2) $
여기서 $c_2$는 두 번째 스케일링 요소입니다.
DSSA의 형태는 VSA 및 기존의 스파이킹 셀프 어텐션 메커니즘과 다르기 때문에, DSSA가 어떻게 셀프 어텐션을 달성하는지에 대한 추가 논의는 보충 자료에서 다루고 있습니다.
여기까지 내용을 다시 요약 정리해보면 아래와 같다.
1. 기존의 셀프 어텐션 문제
먼저, 일반적인 인공신경망(ANN)에서 사용하는 셀프 어텐션은 다음과 같은 수식으로 표현됩니다:
$$
\text{Attention}(Q, K, V) = \text{Softmax}\left(\frac{QK^T}{\sqrt{d}}\right)V
$$
여기서 $ Q $ (Query), $ K $ (Key), 그리고 $ V $ (Value)는 각각 데이터를 변환한 값이고, $ \frac{QK^T}{\sqrt{d}}$는 Query와 Key 사이의 관계를 계산하는 부분이에요. Softmax는 값을 확률처럼 만들기 위한 함수인데, 이 과정에서 부동 소수점 연산(실수 계산)이 많이 발생합니다.
하지만 SNN에서는 이런 실수 연산이 힘들어요. SNN은 스파이크(0 또는 1)로 계산을 하기 때문에, 부동 소수점 연산을 쓰면 에너지가 많이 들고 효율이 떨어지게 돼요.
2. DSSA의 핵심 개념
DSSA는 이러한 문제를 해결하기 위해 설계된 새로운 스파이킹 셀프 어텐션 메커니즘이에요. **DSSA**의 핵심은 **Dual Spike Transformation (DST)**를 사용하는 거예요.
DST는 두 스파이크 행렬 \( X \)와 \( Y \) 사이에서 다음과 같은 변환을 수행합니다:
$$
\text{DST}(X, Y; f(\cdot)) = Xf(Y) = XYW
$$
여기서 $X$와 $Y$는 각각 이진 스파이크 행렬로, $0$ 또는 $1$ 값을 가집니다. **행렬 곱셈**을 수행하지만, 실제로는 부동 소수점 곱셈이 아니라 **스파이크 값을 이용한 논리적 연산**이에요. 즉, 두 값이 모두 1일 때만 1이 되고, 나머지 경우는 0이 됩니다. 이 방식은 곱셈 대신 덧셈으로 처리돼서 계산이 훨씬 간단해져요.
3. 스파이킹 어텐션 맵 (Spiking Attention Map)
DST를 통해 얻어진 어텐션 맵은 다음과 같이 정의됩니다:
$$
\text{AttnMap}(X) = \text{SN}(\text{DST}^T(X, X; f(\cdot)) \ast c_1)
$$
여기서 **DST^T**는 행렬의 전치(transpose)를 적용한 DST 연산이고, **SN**은 스파이킹 뉴런 레이어를 의미합니다. 이 과정에서 소프트맥스처럼 복잡한 계산 대신 **이진 스파이크 연산**으로 간단하게 어텐션을 계산합니다.
4. DSSA의 전체 동작
DSSA는 다음과 같이 전체 어텐션 메커니즘을 정의합니다:
$$
\text{DSSA}(X) = \text{SN}(\text{DST}(\text{AttnMap}(X), X; f(\cdot)) \ast c_2)
$$
여기서, $X$는 입력 데이터, $f(\cdot)$는 변환 함수, 그리고 $c_2$는 스케일링 요소입니다. 이 연산에서 부동 소수점 계산을 전혀 사용하지 않고, 스파이크 값으로만 어텐션을 수행할 수 있습니다.
5. 결론
DSSA는 기존의 ANN 셀프 어텐션과 달리 **부동 소수점 곱셈**이나 **소프트맥스 연산**을 사용하지 않고, **스파이크 기반의 이진 연산**만으로 어텐션을 수행합니다. 이는 계산 효율성을 크게 높이고, SNN에서 더 적합하게 동작할 수 있도록 설계된 방식입니다.

4.3 Scaling Factors in DSSA
DSSA는 SNN에서의 셀프 어텐션 메커니즘을 도입할 때, 각 뉴런의 스파이크 활성화를 적절히 조절하기 위해 스케일링 요소를 사용한다.
1. 왜 스케일링이 중요한가?
기존의 셀프 어텐션 메커니즘에서, 행렬 $$Q$$와 $$K$$의 곱셈 결과는 차원이 커짐에 따라 값이 매우 커질 수 있어요. 그래서 보통 다음과 같이 스케일링을 해줍니다:
$$ \frac{QK^T}{\sqrt{d}}$$
여기서 $d$는 임베딩 차원입니다. 이렇게 스케일링을 하지 않으면, 값이 너무 커지거나 작아져서 학습 과정에서 그레이디언트 소실(gradient vanishing)이나 폭발(exploding) 문제가 발생할 수 있어요. 즉, 적절한 스케일링은 학습의 안정성을 보장하는 중요한 역할을 합니다.
2. DSSA에서는 어떻게 적용되나요?
DSSA에서도 스케일링 요소가 필요해요. 하지만 기존의 셀프 어텐션처럼 단순하게 $\frac{1}{\sqrt{d}}$를 적용할 수 없어요. 그 이유는 DSSA의 입력은 **스파이크 신호(0 또는 1)**로, 값의 평균이 0이고 분산이 1인 실수 값들이 아니기 때문이에요.
DSSA에서는 스파이크 입력의 특성에 맞게 스케일링 요소를 정의해야 해요. 여기서는 두 가지 중요한 스케일링 요소가 등장합니다:
- 첫 번째 스케일링 요소 $c_1$: 어텐션 맵을 계산할 때 사용됩니다.
- 두 번째 스케일링 요소 $c_2$: 최종 출력을 계산할 때 사용됩니다.
이 스케일링 요소들은 각각 **입력 스파이크 행렬의 발화 비율(average firing rate)**에 따라 다르게 계산됩니다.
1. Theorem 1: 스파이크 행렬의 평균과 분산
Theorem 1은 **Dual Spike Transformation (DST)**에 대한 설명이에요. 즉, 두 개의 스파이크 행렬 \( X \)와 \( Y \)가 있을 때, 이들의 행렬 곱셈 결과 \( I \)가 어떤 특성을 가지는지를 수학적으로 분석한 거예요. 정리는 다음과 같이 표현됩니다:
##### Theorem 1 (Mean and variance of DST)
Given spike input $ X \in \{0, 1\}^{T \times p \times m} $,
$ Y \in \{0, 1\}^{T \times m \times q} $, and
a linear transformation $ f(\cdot) $ with weight matrix $ W \in \mathbb{R}^{q \times q} $,
the output of DST, $ I \in \mathbb{R}^{T \times p \times q} $, can be expressed as follows:
$$ I = \text{DST}(X, Y; f(\cdot)) = XYW $$
- 여기서, $ X $와 $ Y $는 스파이크 신호(0 또는 1)로 이루어진 행렬이고, $W$는 가중치 행렬입니다.
- 이때, $ I $는 DST 변환의 결과로 얻어진 출력입니다.
$ I $의 **평균**과 **분산**을 계산할 수 있음을 보여줍니다.
평균과 분산:
- **평균 (Mean):** $$ E(I_{i,j}[t]) = 0 $$
- 이는 스파이크 신호에서 평균적으로 계산된 값이 0이라는 뜻이에요. 스파이크 행렬은 0과 1로 이루어져 있는데, 전체적으로는 균형이 맞아 떨어져서 평균이 0이 됩니다.
- **분산 (Variance):** $$ \text{Var}(I_{i,j}[t]) = f_X m $$
- 여기서 $$ f_X $$는 스파이크 입력 $$ X $$의 **발화 비율(firing rate)**을 의미하고, $$ m $$은 스파이크 행렬의 크기와 관련된 요소입니다.
- 즉, 이 식은 행렬 곱셈 결과가 얼마나 흩어져 있는지를 나타내며, 발화 비율에 따라 분산이 결정됩니다.
이 정리는 스파이킹 뉴런 간의 상호작용에서 발생하는 행렬 곱셈의 평균과 분산을 명확하게 정의함으로써, 이를 바탕으로 적절한 **스케일링 요소**를 설계할 수 있게 해줍니다.
2. 스케일링 요소의 의미
Theorem 1에서 얻은 결과를 바탕으로 DSSA에서 사용되는 **스케일링 요소**들을 정의할 수 있어요. 이전 설명에서 이야기한 것처럼, DSSA는 두 가지 중요한 스케일링 요소를 사용합니다:
1. 첫 번째 스케일링 요소 $$ c_1 $$:
- $$ c_1 = \frac{1}{\sqrt{f_X d}} $$
- 여기서 $$ f_X $$는 스파이크 행렬 $$ X $$의 발화 비율, $$ d $$는 임베딩 차원입니다.
- 이 스케일링 요소는 DSSA에서 **어텐션 맵**을 계산할 때 사용되며, 발화 비율을 고려하여 값이 너무 커지지 않도록 조정합니다.
2. 두 번째 스케일링 요소 $$ c_2 $$:
- $$ c_2 = \frac{1}{\sqrt{f_{Attn} HW/p^2}} $$
- 여기서 $$ f_{Attn} $$은 어텐션 맵의 발화 비율, $$ H $$와 $$ W $$는 공간적 크기, $$ p $$는 합성곱(Convolution) 필터 크기입니다.
- 이 스케일링 요소는 DSSA의 최종 출력을 계산할 때 사용됩니다.
스케일링 요소는 발화 비율과 공간적 차원에 맞게 값들을 조정해 주는 역할을 합니다. 이는 SNN에서 값이 너무 크거나 작아지는 문제를 방지하고, 안정적인 학습을 가능하게 해줍니다.
3. 결론
DSSA의 스케일링 요소는 기존 ANN 셀프 어텐션처럼 단순히 차원에 따라 적용되는 것이 아니라, 스파이크 발화 비율과 데이터의 특성에 따라 정교하게 조정된다는 점이 특징이에요.
Theorem 1은 DSSA에서 스케일링 요소를 정확하게 계산하기 위한 수학적 기반을 제공합니다. 스파이킹 행렬의 평균과 분산을 계산함으로써, DSSA가 다양한 입력 크기와 발화 비율에 맞게 스케일링을 조정할 수 있게 됩니다. 이로 인해 SNN에서 안정적인 학습이 가능하고, 최적의 성능을 유지할 수 있습니다.
4.4. Spike-driven Characteristic of DSSA
스파이크 구동 특성은 SNN(Spiking Neural Networks)에 매우 중요합니다. 즉, 계산은 스파이크로 인해 간헐적으로 발생하며, 시냅스 연산만을 요구합니다. 이전 연구들에서는 스파이크 구동 트랜스포머를 구현하기 위해 많은 노력을 기울였습니다. 이 절에서는 DSSA의 스파이크 구동 특성을 깊이 있게 논의하고, DSSA가 스파이크 구동 방식으로 동작함을 증명합니다. 먼저, 스파이크 구동 특성에 대한 공식적인 정의를 제시합니다.
#### 정의 1 SNN이 스파이크 구동 방식으로 동작한다면, 모든 뉴런의 입력 전류는 다음과 같은 형태를 가져야 합니다:
$ I_i[t] = \sum_j w_{i,j}s_j[t] = \sum_{j, s_j[t] \neq 0} w_{i,j} $
여기서 $$ I_i[t] $$는 $$ t $$ 시점에서 $$ i $$-번째 포스트시냅스 뉴런의 입력 전류를 나타내고, $$ s_j[t] \in \{0, 1\} $$는 $$ j $$-번째 프리시냅스 뉴런의 스파이크 출력, $$ w_{i,j} $$는 뉴런 $$ j $$에서 뉴런 $$ i $$로의 시냅스 연결 가중치를 나타냅니다.
이 정의는 스파이크 구동 특성의 본질을 설명합니다.
즉, 입력 전류의 누적은 프리시냅스 뉴런에서 발생한 스파이크에 의해 간헐적으로 발생합니다.
흔히 사용되는 선형 계층과 합성곱 계층이 이 정의를 만족하는 것이 명확합니다.
DSSA는 스파이킹 뉴런 계층 두 개, 즉 스파이킹 어텐션 맵 계층과 출력 계층만을 포함합니다.
이 두 계층 모두 DST(Dual Spike Transformation)로부터 파생된 입력 전류를 받습니다.
따라서, 우리는 DST가 정의 1의 형태를 만족하는지 확인해야 합니다.
먼저, 식 (8)에서 $$DST^T$$를 검증합니다:
$ I = X W^T Y^T $
이때, $$ I_{i,j}[t] $$는 다음과 같이 표현됩니다:
$ I_{i,j}[t] = \sum_{k=1}^{m} \sum_{l=1}^{m} x_{i,k}[t] w_{l,k} y_{j,l}[t] = \sum_{k,l} (x_{i,k}[t] \land y_{j,l}[t] \neq 0) w_{l,k} $
여기서 약간의 차이가 있지만, 스파이크 입력은 듀얼 스파이크의 논리적 AND로 간주될 수 있습니다.
이는 듀얼 스파이크가 트리거되어야 하는 시냅스 연산으로 해석될 수 있으며, 이를 듀얼 스파이크 변환(Dual Spike Transformation)이라고 부르는 이유입니다.
마찬가지로, 식 (7)에서 DST도 다음과 같이 표현할 수 있습니다:
$ I = X Y W $
$ I_{i,j}[t] = \sum_{k=1}^{m} \sum_{l=1}^{q} x_{i,k}[t] y_{k,l}[t] w_{l,j} = \sum_{k,l} (x_{i,k}[t] \land y_{k,l}[t] \neq 0) w_{l,j} $
따라서, DSSA는 스파이크 구동 방식으로 동작합니다.
5. SpikingResformer
이 섹션에서는 제안된 SpikingResformer 아키텍처를 소개합니다. SpikingResformer는 ResNet 기반의 다단계 설계와 DSSA(Dual Spike Self-Attention)를 결합하여 더 효율적인 SNN(Spiking Neural Network)을 구현한 모델입니다. SpikingResformer는 더 적은 파라미터로 더 높은 정확도를 달성하며, 기존의 스파이킹 비전 트랜스포머와 비교해 에너지 소비도 감소시킵니다.
SpikingResformer는 기존 ResNet의 장점을 살리면서도 SNN에 적합한 방식으로 트랜스포머 구조를 통합한 것이 특징입니다. 특히, 여러 스테이지로 나누어 학습의 효율성과 성능을 극대화합니다.

5.1. Overall Architecture
SEW ResNet [9], Spikformer [45], 그리고 제안된 SpikingResformer의 전체 구조는 그림 2에 나와 있습니다. 그림 2에서 볼 수 있듯이, Spikformer는 Spiking Patch Splitting(SPS) 모듈을 사용하여 이미지를 공간 크기가 줄어든 후 d 차원의 특징으로 투영합니다. 그러나 얕은 스파이킹 컨볼루션 모듈로는 로컬 정보를 잘 모델링할 수 없고, 단일 스케일의 특징 맵만 생성합니다. 반면에, SEW ResNet은 Spikformer의 SPS보다 훨씬 깊고, 다단계 아키텍처로 다중 스케일의 특징을 추출하는 데 더 뛰어난 성능을 보이지만, 글로벌 정보를 추출하는 데 도움이 되는 셀프 어텐션 메커니즘이 부족합니다. 이러한 아키텍처의 한계를 극복하고 그 장점을 활용하기 위해, 우리는 ResNet 기반 아키텍처와 스파이킹 셀프 어텐션 메커니즘을 결합한 SpikingResformer를 제안합니다.
SpikingResformer 시리즈의 전체 구조에 대한 세부 사항은 표 1에 나와 있습니다.
ResNet 기반 SNN [9, 14]과 유사하게, 우리의 모델은 7×7 컨볼루션과 3×3 맥스 풀링으로 구성된 스템 아키텍처로 시작하여 로컬화된 특징을 미리 추출하고, 다단계 백본을 사용하여 다중 스케일의 특징 맵을 생성합니다.
각 단계에서는 여러 스파이킹 Resformer 블록이 순차적으로 쌓여 있습니다. 각 스파이킹 Resformer 블록은 두 가지 모듈로 구성되며, 각각 Multi-Head Dual Spike Self-Attention (MHDSSA) 블록과 Group-Wise Spiking Feed-Forward Network (GWSFFN)로 불립니다. 다운샘플링 계층은 각 단계 전에 적용되어 특징 맵의 크기를 줄이고 더 높은 차원으로 투영합니다 (해상도를 2배 다운샘플링하고 차원을 2배로 확장). 마지막으로, 모델은 글로벌 평균 풀링 레이어와 분류 레이어로 끝납니다.
5.2. Spiking Resformer Block
그림 2에서 볼 수 있듯이, 스파이킹 Resformer 블록은 1.Multi-Head Dual Spike Self-Attention (MHDSSA) 모듈과 2.Group-Wise Spiking Feed-Forward Network (GWSFFN)로 구성됩니다. 우리는 먼저 두 모듈을 소개한 후, 스파이킹 Resformer 블록의 형태를 도출합니다.
1.Multi-Head Dual Spike Self-Attention (MHDSSA)
섹션 4장에서 우리는 DSSA의 싱글 헤드 형태를 제안했습니다. 이는 기본 Transformer와 유사한 접근 방식을 따라 멀티 헤드 DSSA(MHDSSA)로 쉽게 확장될 수 있습니다. MHDSSA에서 우리는 먼저 DST에서 선형 변환의 결과를 $$h$$개의 헤드로 나누고, 각 헤드에 DSSA를 수행한 후 이를 결합합니다. 마지막으로, 포인트 와이즈 컨볼루션을 사용하여 결합된 특징을 원래 공간으로 투영하여 다른 헤드에서 나온 특징을 융합합니다.
MHDSSA는 다음과 같이 수식화할 수 있습니다:
$ \text{ MHDSSA(X)} = \text{BN}( \text{Conv}_1([ \text{DSSA}_i( \text{SN}(X))]^h_{i=1})) $
여기서 $$[ \cdot ]$$는 결합(concatenate) 연산을 나타내며, $$\text{Conv}_1$$은 포인트 와이즈 컨볼루션을 나타냅니다.
2.Group-Wise Spiking Feed-Forward Network (GWSFFN)
이전 스파이킹 비전 트랜스포머에서 제안된 스파이킹 피드포워드 네트워크(SFFN)는 배치 정규화 및 스파이킹 뉴런 활성화를 가진 두 개의 선형 계층으로 구성됩니다. 또한, 확장 비율은 일반적으로 4로 설정되며, 첫 번째 계층은 차원을 4배로 확장하고 두 번째 계층은 원래 차원으로 축소합니다. SFFN을 기반으로, 우리는 두 선형 계층 사이에 잔차 연결이 있는 3×3 합성곱 계층을 삽입하여 SFFN이 로컬 특징을 추출할 수 있도록 했습니다. 입력에 비해 두 선형 계층 사이의 숨겨진 특징 차원이 4배로 확장되기 때문에, 파라미터 수와 계산 오버헤드를 줄이기 위해 그룹별 합성곱을 사용하고 64개의 채널마다 하나의 그룹으로 설정합니다. 또한, 이전 연구에서 사용된 스파이크 구동 설계를 적용합니다.
그룹별 스파이킹 피드포워드 네트워크(GWSFFN)는 다음과 같이 공식화될 수 있습니다:
$ \text{FFL}_i(X) = \text{BN}(\text{Conv1}(\text{SN}(X))), \quad i = 1, 2, $
$ \text{GWL}(X) = \text{BN}(\text{GWConv}(\text{SN}(X))) + X, $
$ \text{GWSFFN}(X) = \text{FFL}_2(\text{GWL}(\text{FFL}_1(X))). $
여기서, $$ \text{FFL}_i $$는 피드포워드 계층을 나타내며, $$ \text{Conv1} $$는 point-wise convolution (1×1 컨볼루션)으로, 이는 linear transformation 과 같습니다.
$$ \text{GWL} $$은 group-wise convolution layer 나타내며, $$ \text{GWConv} $$는 group-wise convolution을 의미합니다.
Spiking Resformer Block.
위의 MHDSSA 모듈과 GWSFFN을 사용하여, 스파이킹 Resformer 블록은 다음과 같이 공식화할 수 있습니다:
$ Y_i = MHDSSA(X_i) + X_i, $
$ X_{i+1} = GWSFFN(Y_i) + Y_i. $
여기서 $$Y_i$$는 $$i$$번째 스파이킹 Resformer 블록에서 MHDSSA 모듈의 출력 특징을 나타냅니다.

6. Experiments
이 섹션에서는 먼저 SpikingResformer의 ImageNet 분류 작업에서의 성능과 에너지 효율성을 평가합니다. 그 후, SpikingResformer의 핵심 구성 요소에 대한 제거 실험을 수행합니다. 마지막으로, SpikingResformer의 전이 학습 능력을 평가합니다.
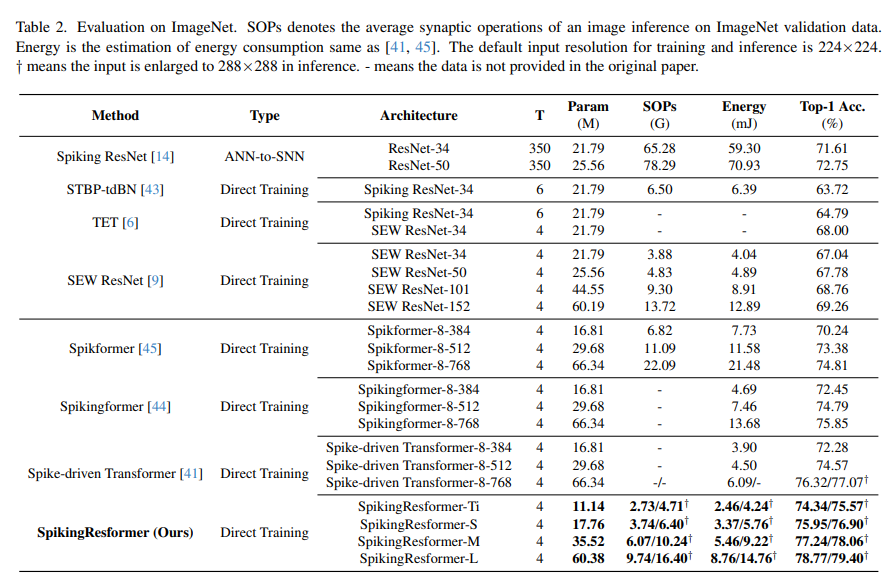
6.1. ImageNet Classification
ImageNet [4]는 이미지 분류에 널리 사용되는 전형적인 정적 이미지 데이터셋 중 하나입니다. 공정한 비교를 위해, 우리는 일반적으로 [41]에서 사용된 데이터 증강 전략과 훈련 설정을 따릅니다. 실험 설정에 대한 자세한 내용은 보충 자료에서 확인할 수 있습니다.
결과. 우리의 실험 결과는 표 2에 나와 있습니다. 비교를 위해, 기존의 스파이킹 컨볼루션 네트워크와 스파이킹 비전 트랜스포머의 결과도 함께 나열했습니다. 표 2에서 볼 수 있듯이, SpikingResformer는 기존 방법에 비해 더 높은 정확도, 더 적은 파라미터, 더 낮은 에너지 소비를 동시에 달성합니다. 예를 들어, SpikingResformer-Ti는 11.14M 파라미터와 2.73G SOPs(2.46mJ)만으로 74.34%의 정확도를 달성하며, Spike-driven Transformer-8-384보다 2.06% 더 높은 정확도와 5.67M 파라미터 및 1.44mJ 에너지를 절약합니다. SpikingResformer-M은 35.52M 파라미터와 6.07G SOPs(5.46mJ)로 77.24%의 정확도를 달성하며, Spike-driven Transformer-8-768보다 0.92% 더 높은 정확도와 30.82M 파라미터를 절약합니다. 특히, SpikingResformer-L은 입력 크기를 288×288으로 확장했을 때 최대 79.40%의 정확도를 달성하여 SNN 분야에서 최첨단 결과를 보여줍니다.
6.2. Ablation Study

우리는 SpikingResformer의 핵심 구성 요소에 대한 ablation experiments을 수행했습니다. 여기에는 multi-stage architecture , GWSFFN의 group-wise convolution layer, 그리고 우리가 제안한 spiking self-attention mechanism이 포함됩니다. ablation experiments은 ImageNet 데이터셋의 100개 카테고리로 구성된 하위 집합인 ImageNet100 데이터셋에서 수행되었습니다. 실험 설정은 대체로 6.1 섹션의 설정을 따르며, 자세한 설정은 보충 자료에 나와 있습니다.
- Multi-Stage Architecture: multi-stage architecture의 효과를 검증하기 위해, Spikingformer 기반 아키텍처로 대체하였으며, spiking Resformer block의 구조는 변경하지 않았습니다. 모델 파라미터를 SpikingResformer-S와 비슷하게 조정했습니다. 표 3에 나타난 것처럼, SpikingResformer-S는 multi-stage architecture가 없는 변형 모델보다 2.74% 더 우수한 성능을 보여 multi-stage architecture의 효과를 입증했습니다.
- Group-Wise Convolution Layer: point-wise SFFN과 비교할 때, GWSFFN은 두 개의 linear layers 사이에 3×3 group-wise convolution layer을 사용합니다. group-wise convolution layer를 제거하고 파라미터 수를 일정하게 유지하기 위해 차원을 증가시키는 방식으로 결를 평가했습니다. 표 3에서 보듯이, SpikingResformer-S는 group-wise convolution layer가 없는 변형 모델보다 3.42% 더 높은 정확도를 달성하였으며, 이는 GWSFFN에서 group-wise convolution layer의 이점을 강조합니다.
- Dual Spike Self-Attention (DSSA): DSSA의 효과를 검증하기 위해, DSSA를 Spikformer의 Spiking Self-Attention(SSA) 및 Spike-driven Transformer의 Spike-Driven Self-Attention(SDSA)으로 교체했습니다. 그러나 SSA와 SDSA는 모두 수렴하지 않았습니다. 이는 SSA와 SDSA가 다중 스케일 입력에 적합하지 않기 때문이라고 생각됩니다. DSSA가 다중 스케일 입력에 맞게 조정되는 주요 요소를 추가로 검증하기 위해, 우리는 두 가지 추가 실험을 수행했습니다. 첫 번째는 DST에서 모든 $$p \times p$$ 합성곱을 $$1 \times 1$$ 합성곱으로 교체하여 공간 크기 축소의 효과를 검증하는 것이었고, 두 번째는 스케일링 요소를 제거하거나 제안한 스케일링 요소를 $$ \frac{1}{\sqrt{d}}$$로 대체하여 스케일링의 효과를 검증하는 것이었습니다. 첫 번째 그룹은 수렴했지만 86.14%의 정확도와 더 높은 에너지 소비(3.91mJ)를 보였고, 두 번째 그룹은 수렴하지 않았습니다. 이는 스케일링 요소가 수렴에 중요한 요소임을 보여줍니다.

6.3. Transfer Learning
전이 학습 능력은 비전 트랜스포머의 주요 장점 중 하나입니다. 우리는 ImageNet에서 사전 학습된 모델을 미세 조정하여, 제안된 SpikingResformer의 전이 학습 능력을 정적 데이터셋인 CIFAR10과 CIFAR100 [19] 및 신경형 데이터셋인 CIFAR10-DVS [23]와 DVSGesture [1]에서 평가했습니다. 기존 스파이킹 비전 트랜스포머 중에서는 Spikformer만이 전이 학습 결과를 제공하며, 그것도 CIFAR10과 CIFAR100 정적 이미지 데이터셋에 한정됩니다. 따라서 우리는 전이 학습 결과와 직접 훈련 결과를 함께 비교하여 포괄적인 비교를 수행했습니다. 표 4에는 이러한 방법들로 달성된 최고 정확도가 나와 있습니다. 실험 설정 및 더 자세한 비교는 보충 자료에서 확인할 수 있습니다.
Static Image Datasets.
표 4에서 볼 수 있듯이, SpikingResformer는 CIFAR10 데이터셋에서 97.40%의 정확도, CIFAR100 데이터셋에서 85.98%의 정확도를 달성하여 최첨단 결과를 보여주었으며, Spikformer의 전이 학습 결과를 CIFAR10에서 0.37%, CIFAR100에서 2.15% 능가했습니다. 직접 훈련 방법과 비교했을 때, 전이 학습을 통해 얻은 SpikingResformer는 훨씬 더 우수한 성능을 보였습니다. 예를 들어, SpikingResformer는 CIFAR100 데이터셋에서 Spikingformer보다 6.89% 더 높은 성능을 보여 전이 학습의 장점을 입증했습니다.
Neuromorphic Datasets.
Neuromorphic datasets 전통적인 정적 이미지 데이터셋과는 크게 다릅니다. 신경형 데이터셋의 샘플은 RGB 이미지 대신 이벤트 스트림으로 구성됩니다. 그 결과, 정적 이미지 데이터셋에서 사전 학습된 모델과 타겟 도메인 간의 큰 차이가 발생합니다. 이 격차를 해소하기 위해, 우리는 일정 기간 동안 이벤트를 쌓아 프레임을 형성했습니다. RGB 채널은 각각 양의 이벤트, 음의 이벤트, 이벤트 합계 채널로 대체되었습니다. 표 4에서 볼 수 있듯이, SpikingResformer의 전이 학습 결과는 CIFAR10-DVS에서 직접 훈련된 결과를 크게 능가합니다. SpikingResformer는 CIFAR10-DVS에서 84.8%의 정확도를 달성했으며, Spikingformer보다 3.5% 높은 성능을 보였습니다. 그러나 DVSGesture에서 전이 학습 결과는 직접 훈련 성능에 비해 비교 가능한 성과를 거두지 못했습니다. SpikingResformer는 DVSGesture에서 93.4%의 정확도를 달성했지만, 최첨단 방법인 Spike-driven Transformer보다 5.9% 뒤처졌습니다. 이는 주로 CIFAR10-DVS와 DVSGesture가 구성되는 방식의 차이 때문이라고 생각됩니다. CIFAR10-DVS는 CIFAR10에서 변환된 것이며, 시간 정보를 포함하지 않습니다. 따라서 정적 데이터셋에서 사전 학습된 모델은 CIFAR10-DVS로 잘 전이됩니다. 그러나 DVSGesture는 다이나믹 비전 센서를 사용하여 인간의 제스처에서 직접 생성된 것으로, 풍부한 시간 정보를 포함하고 있습니다. 그 결과, 정적 데이터셋에서 사전 학습된 모델은 DVSGesture로 잘 전이되지 않습니다. 우리는 신경형 데이터셋에서의 전이 학습에 대한 우리의 탐구가 SNN의 전이 학습 연구를 위한 길을 열 수 있기를 바랍니다.
7. Conclusion
이 논문에서 우리는 Dual Spike Self-Attention (DSSA)이라는 새로운 스파이킹 셀프 어텐션 메커니즘을 제안합니다. DSSA는 Dual Spike Transformation을 통해 스파이킹 셀프 어텐션을 생성하며, 이는 완전히 스파이크 구동 방식으로 동작하며 SNN과 호환됩니다. 우리는 DSSA에서 다양한 스케일의 특징 맵을 처리할 수 있도록 해주는 스케일링 요소를 상세히 설명했습니다. DSSA를 기반으로, 우리는 ResNet 기반 다단계 아키텍처와 DSSA를 결합한 SpikingResformer를 제안하였으며, 이를 통해 더 적은 파라미터로 우수한 성능과 에너지 효율성을 달성할 수 있었습니다. 광범위한 실험을 통해 제안된 SpikingResformer의 효율성과 우수성이 입증되었습니다.

먼저 저자의 깃허브에 설치 사항을 그대로 따라하면 무조건 오류가 뜬다.
나는 cuda12라서 cupy-cuda11x를 하면 나중에 오류가 났다. 자신의 cuda에 맞게 cupy를 설치 할것
spikingjelly의 경우 위 버전을 다운받으면 아래와 같은 오류가 발생할 수 있다.
Exception has occurred: AttributeError
module 'numpy' has no attribute 'int'.
np.int was a deprecated alias for the builtin int. To avoid this error in existing code, use int by itself. Doing this will not modify any behavior and is safe. When replacing np.int, you may wish to use e.g. np.int64 or np.int32 to specify the precision. If you wish to review your current use, check the release note link for additional information.
The aliases was originally deprecated in NumPy 1.20; for more details and guidance see the original release note at:
https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations
File "E:\SpikingResformer\models\spikingresformer.py", line 74, in forward
x = self.activation_in(x)
File "E:\SpikingResformer\models\spikingresformer.py", line 203, in forward
x = self.layers(x)
File "E:\SpikingResformer\main_custom.py", line 427, in train_one_epoch
output = model(image)
File "E:\SpikingResformer\main_custom.py", line 751, in main
train_loss, train_acc1, train_acc5 = train_one_epoch(model, criterion, optimizer,
File "E:\SpikingResformer\main_custom.py", line 832, in <module>
main()
AttributeError: module 'numpy' has no attribute 'int'.
np.int was a deprecated alias for the builtin int. To avoid this error in existing code, use int by itself. Doing this will not modify any behavior and is safe. When replacing np.int, you may wish to use e.g. np.int64 or np.int32 to specify the precision. If you wish to review your current use, check the release note link for additional information.
The aliases was originally deprecated in NumPy 1.20; for more details and guidance see the original release note at:
https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations이는 numpy 1.20부터 np.int가 없는데 spikingjelly 라이브러리 내에 np.int를 사용하는 부분이 있어서 그렇다.
따라서 최신버전을 다운 받거나 아래와 같이 github의 setup.py를 통해 다운 받아야 한다.
https://pypi.org/project/spikingjelly/
[spikingjelly
A deep learning framework for SNNs built on PyTorch.
pypi.org](https://pypi.org/project/spikingjelly/)
그럼 이제 제대로 모델을 훈련해보자. main.py를 수행하는데 아래와 같은 코드를 먼저 수행해보자.
main.py -c configs/direct_training/cifar10.yaml다음으로 main.py를 실행하면 아래와 같은 오류가 발생할 수 있다.
FutureWarning: torch.cuda.amp.autocast(args...) is deprecated. Please use torch.amp.autocast('cuda', args...) instead.
with autocast():이부분은 아래와 같이 바꿔줘야 한다.
from torch.amp import GradScaler, autocast그리고 아래와 같이 cuda를 넣어준다.
with autocast('cuda')configs/direct_training/cifar10.yaml 파일에서 config를 조정하자


잘 돌아간다.
'Paper Review' 카테고리의 다른 글
| SNN의 약점을 개선해 나가고 있는 방법들 (0) | 2024.09.14 |
|---|---|
| [SpikeFormer 논문리뷰] SPIKFORMER: WHEN SPIKING NEURAL NETWORK MEETS TRANSFORMER (0) | 2024.08.22 |
| Neural Transformation Learning for Deep Anomaly Detection Beyond Images (0) | 2024.05.17 |
| Deep SVDD (1) | 2024.05.17 |
| GOAD: CLASSIFICATION-BASED ANOMALY DETECTION FORGENERAL DATA (0) | 2024.05.17 |
소중한 공감 감사합니다